PyTorch#
Environment setup#
import platform
print(f"Python version: {platform.python_version()}")
assert platform.python_version_tuple() >= ("3", "6")
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
import seaborn as sns
Python version: 3.7.5
# Setup plots
%matplotlib inline
plt.rcParams["figure.figsize"] = 10, 8
%config InlineBackend.figure_format = 'retina'
sns.set()
%load_ext tensorboard
import sklearn
print(f"scikit-learn version: {sklearn.__version__}")
from sklearn.datasets import make_moons
import torch
print(f"PyTorch version: {torch.__version__}")
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
import torchvision
import torchvision.transforms as transforms
from torch.utils.tensorboard import SummaryWriter
scikit-learn version: 0.22.1
PyTorch version: 1.3.1
Show code cell source
def plot_planar_data(X, y):
"""Plot some 2D data"""
plt.figure()
plt.plot(X[y == 0, 0], X[y == 0, 1], 'or', alpha=0.5, label=0)
plt.plot(X[y == 1, 0], X[y == 1, 1], 'ob', alpha=0.5, label=1)
plt.legend()
Tensor API#
Tensor creation#
# Create 1D tensor with predefined values
t = torch.tensor([5.5, 3])
print(t)
print(t.shape)
tensor([5.5000, 3.0000])
torch.Size([2])
# Create 2D tensor filled with random numbers from a uniform distribution
x = torch.rand(5, 3)
print(x)
print(x.shape)
tensor([[0.3746, 0.1669, 0.0174],
[0.9889, 0.9538, 0.0463],
[0.1561, 0.4398, 0.5971],
[0.9370, 0.8256, 0.6580],
[0.2451, 0.8639, 0.5963]])
torch.Size([5, 3])
Operations#
# Addition operator
y = x + 2
print(y)
tensor([[2.3746, 2.1669, 2.0174],
[2.9889, 2.9538, 2.0463],
[2.1561, 2.4398, 2.5971],
[2.9370, 2.8256, 2.6580],
[2.2451, 2.8639, 2.5963]])
# Addition method
y = torch.add(x, 2)
print(y)
tensor([[2.3746, 2.1669, 2.0174],
[2.9889, 2.9538, 2.0463],
[2.1561, 2.4398, 2.5971],
[2.9370, 2.8256, 2.6580],
[2.2451, 2.8639, 2.5963]])
y = torch.zeros(5, 3)
# In-place addition: tensor is mutated
y.add_(x)
y.add_(2)
print(y)
tensor([[2.3746, 2.1669, 2.0174],
[2.9889, 2.9538, 2.0463],
[2.1561, 2.4398, 2.5971],
[2.9370, 2.8256, 2.6580],
[2.2451, 2.8639, 2.5963]])
Indexing#
print(x)
# Print second column of tensor
print(x[:, 1])
tensor([[0.3746, 0.1669, 0.0174],
[0.9889, 0.9538, 0.0463],
[0.1561, 0.4398, 0.5971],
[0.9370, 0.8256, 0.6580],
[0.2451, 0.8639, 0.5963]])
tensor([0.1669, 0.9538, 0.4398, 0.8256, 0.8639])
Reshaping with view()#
PyTorch allows a tensor to be a view of an existing tensor. For memory efficiency reasons, view tensors share the same underlying data with their base tensor.
# Reshape into a (15,) vector
x.view(15)
tensor([0.3746, 0.1669, 0.0174, 0.9889, 0.9538, 0.0463, 0.1561, 0.4398, 0.5971,
0.9370, 0.8256, 0.6580, 0.2451, 0.8639, 0.5963])
# The dimension identified by -1 is inferred from other dimensions
print(x.view(-1, 5)) # Shape: (3,5)
print(x.view(5, -1)) # Shape: (5, 3)
print(x.view(-1,)) # Shape: (15,)
# Error: a tensor of size 15 can't be reshaped into a (?, 4) tensor
# print(x.view(-1, 4))
tensor([[0.3746, 0.1669, 0.0174, 0.9889, 0.9538],
[0.0463, 0.1561, 0.4398, 0.5971, 0.9370],
[0.8256, 0.6580, 0.2451, 0.8639, 0.5963]])
tensor([[0.3746, 0.1669, 0.0174],
[0.9889, 0.9538, 0.0463],
[0.1561, 0.4398, 0.5971],
[0.9370, 0.8256, 0.6580],
[0.2451, 0.8639, 0.5963]])
tensor([0.3746, 0.1669, 0.0174, 0.9889, 0.9538, 0.0463, 0.1561, 0.4398, 0.5971,
0.9370, 0.8256, 0.6580, 0.2451, 0.8639, 0.5963])
Reshaping à la NumPy#
# Reshape into a (3,5) tensor, creating a view if possible
x.reshape(3, 5)
tensor([[0.3746, 0.1669, 0.0174, 0.9889, 0.9538],
[0.0463, 0.1561, 0.4398, 0.5971, 0.9370],
[0.8256, 0.6580, 0.2451, 0.8639, 0.5963]])
From NumPy to PyTorch#
# Create a NumPy tensor
a = np.random.rand(2, 2)
# Convert it into a PyTorch tensor
b = torch.from_numpy(a)
print(b)
# a and b share memory
a *= 2
print(b)
b += 1
print(a)
tensor([[0.6285, 0.2705],
[0.8091, 0.1353]], dtype=torch.float64)
tensor([[1.2571, 0.5411],
[1.6182, 0.2706]], dtype=torch.float64)
[[2.25707965 1.54108591]
[2.61824455 1.27061508]]
From PyTorch to NumPy#
# Create a PyTorch tensor
a = torch.rand(2,2)
# Convert it into a NumPy tensor
b = a.numpy()
print(b)
# a and b share memory
a *= 2
print(b)
b += 1
print(a)
[[0.05700839 0.8589342 ]
[0.8565902 0.6768685 ]]
[[0.11401677 1.7178684 ]
[1.7131804 1.353737 ]]
tensor([[1.1140, 2.7179],
[2.7132, 2.3537]])
GPU-based tensors#
# Look for an available CUDA device
if torch.cuda.is_available():
device = torch.device("cuda")
# Move an existing tensor to GPU
x_gpu = x.to(device)
print(x_gpu)
# Directly create a tensor on GPU
t_gpu = torch.ones(3, 3, device=device)
print(t_gpu)
else:
print("No CUDA device available :(")
No CUDA device available :(
# Try to copy tensor to GPU, fall back on CPU instead
device = torch.device('cuda' if torch.cuda.is_available() else 'cpu')
x_device = x.to(device)
print(x_device)
tensor([[0.3746, 0.1669, 0.0174],
[0.9889, 0.9538, 0.0463],
[0.1561, 0.4398, 0.5971],
[0.9370, 0.8256, 0.6580],
[0.2451, 0.8639, 0.5963]])
Neural networks API#
Building models with PyTorch#
The torch.nn package provides the basic building blocks for assembling models. Other packages like torch.optim and torchvision define training utilities and specialized tools.
PyTorch offers a great deal of flexibility for creating custom architectures and training loops, hence its popularity among researchers.
Example 1: training a dense network on planar data#
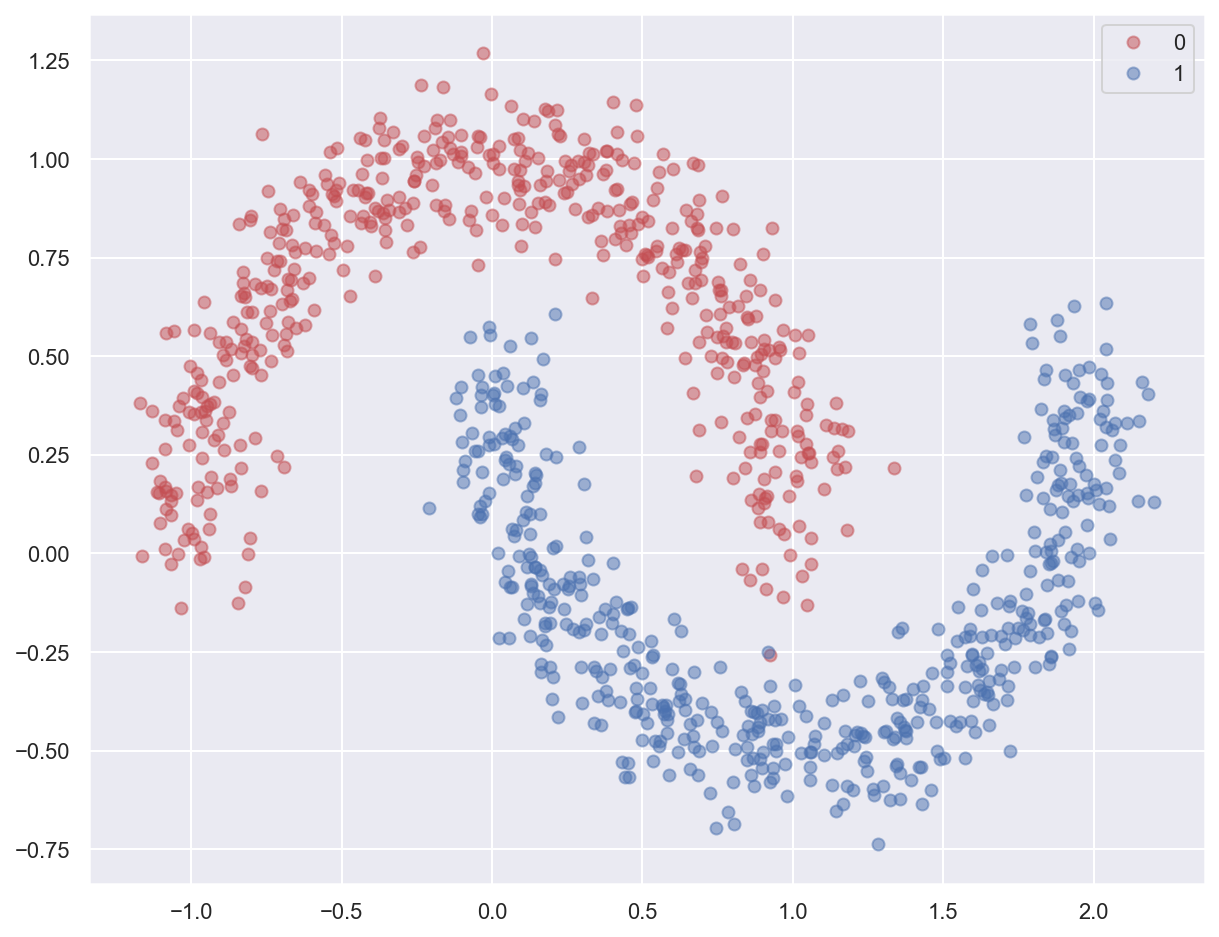
# Generate moon-shaped, non-linearly separable data
x, y = make_moons(n_samples=1000, noise=0.10, random_state=0)
print(f'x: {x.shape}. y: {y.shape}')
plot_planar_data(x, y)
x: (1000, 2). y: (1000,)
# Create PyTorch tensors from Numpy data, with appropriate types
x_train = torch.from_numpy(x).float()
y_train = torch.from_numpy(y).long()
Model definition#
# Use the nn package to define our model as a sequence of layers. nn.Sequential
# is a Module which contains other Modules, and applies them in sequence to
# produce its output. Each Linear Module computes output from input using a
# linear function, and holds internal Tensors for its weight and bias.
dense_model = nn.Sequential(
nn.Linear(in_features=2, out_features=3),
nn.Tanh(),
nn.Linear(in_features=3, out_features=2)
)
print(dense_model)
Sequential(
(0): Linear(in_features=2, out_features=3, bias=True)
(1): Tanh()
(2): Linear(in_features=3, out_features=2, bias=True)
)
# The nn package also contains definitions of popular loss functions; in this
# case we will use Cross Entropy as our loss function.
loss_fn = nn.CrossEntropyLoss()
# Used to enable training analysis through TensorBoard
# Writer will output to ./runs/ directory by default
writer = SummaryWriter()
Model training#
learning_rate = 1.0
num_epochs = 2000
for epoch in range(num_epochs):
# Forward pass: compute model prediction
y_pred = dense_model(x_train)
# Compute and print loss
loss = loss_fn(y_pred, y_train)
if epoch % 100 == 0:
print(f"Epoch [{epoch+1:4}/{num_epochs}], loss: {loss:.6f}")
# Write epoch loss for TensorBoard
writer.add_scalar("Loss/train", loss.item(), epoch)
# Zero the gradients before running the backward pass
# Avoids accumulating gradients erroneously
dense_model.zero_grad()
# Backward pass: compute gradient of the loss w.r.t all the learnable parameters of the model
loss.backward()
# Update the weights using gradient descent
# no_grad() avoids tracking operations history here
with torch.no_grad():
for param in dense_model.parameters():
param -= learning_rate * param.grad
print(f"Training finished. Final loss: {loss:.6f}")
Epoch [ 1/2000], loss: 0.615728
Epoch [ 101/2000], loss: 0.255993
Epoch [ 201/2000], loss: 0.254656
Epoch [ 301/2000], loss: 0.253930
Epoch [ 401/2000], loss: 0.253383
Epoch [ 501/2000], loss: 0.252850
Epoch [ 601/2000], loss: 0.252219
Epoch [ 701/2000], loss: 0.251364
Epoch [ 801/2000], loss: 0.250020
Epoch [ 901/2000], loss: 0.165510
Epoch [1001/2000], loss: 0.034935
Epoch [1101/2000], loss: 0.018792
Epoch [1201/2000], loss: 0.013152
Epoch [1301/2000], loss: 0.010341
Epoch [1401/2000], loss: 0.008661
Epoch [1501/2000], loss: 0.007542
Epoch [1601/2000], loss: 0.006741
Epoch [1701/2000], loss: 0.006137
Epoch [1801/2000], loss: 0.005665
Epoch [1901/2000], loss: 0.005284
Training finished. Final loss: 0.004974
Example 2: training a convnet on CIFAR10#
Data loading and preparation#
# Transform images of range [0, 1] into tensors of normalized range [-1, 1]
transform = transforms.Compose(
[transforms.ToTensor(),
transforms.Normalize((0.5, 0.5, 0.5), (0.5, 0.5, 0.5))])
# Load training set
trainset = torchvision.datasets.CIFAR10(
root="./data", train=True, download=True, transform=transform
)
# Get an iterable from training set
trainloader = torch.utils.data.DataLoader(
trainset, batch_size=4, shuffle=True, num_workers=2
)
testset = torchvision.datasets.CIFAR10(
root="./data", train=False, download=True, transform=transform
)
testloader = torch.utils.data.DataLoader(
testset, batch_size=4, shuffle=False, num_workers=2
)
Files already downloaded and verified
Files already downloaded and verified
Expected network architecture#
# Define a CNN that takes (3, 32, 32) tensors as input (channel-first)
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(in_channels=3, out_channels=6, kernel_size=5)
self.pool = nn.MaxPool2d(kernel_size=2, stride=2)
self.conv2 = nn.Conv2d(in_channels=6, out_channels=16, kernel_size=5)
# Convolution output is 16 5x5 feature maps, flattened as a 400 elements vectors
self.fc1 = nn.Linear(in_features=16 * 5 * 5, out_features=120)
self.fc2 = nn.Linear(in_features=120, out_features=10)
def forward(self, x):
x = self.pool(F.relu(self.conv1(x)))
x = self.pool(F.relu(self.conv2(x)))
x = x.view(-1, 16 * 5 * 5)
x = F.relu(self.fc1(x))
x = self.fc2(x)
return x
cnn_model = Net()
print(cnn_model)
Net(
(conv1): Conv2d(3, 6, kernel_size=(5, 5), stride=(1, 1))
(pool): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False)
(conv2): Conv2d(6, 16, kernel_size=(5, 5), stride=(1, 1))
(fc1): Linear(in_features=400, out_features=120, bias=True)
(fc2): Linear(in_features=120, out_features=10, bias=True)
)
Model training#
criterion = nn.CrossEntropyLoss()
optimizer = optim.SGD(cnn_model.parameters(), lr=0.001, momentum=0.9)
num_epochs = 2
# Loop over the dataset multiple times
for epoch in range(num_epochs):
running_loss = 0.0
for i, data in enumerate(trainloader, 0):
# Get the inputs; data is a list of [inputs, labels]
# inputs is a 4D tensor of shape (batch size, channels, rows, cols)
# labels is a 1D tensor of shape (batch size,)
inputs, labels = data
# Reset the parameter gradients
optimizer.zero_grad()
# Forward pass
outputs = cnn_model(inputs)
# Loos computation
loss = criterion(outputs, labels)
# Backward pass
loss.backward()
# GD step
optimizer.step()
# Print statistics
running_loss += loss.item()
if i % 2000 == 1999: # print every 2000 mini-batches
print(
f"Epoch [{epoch+1}/{num_epochs}], batch {i+1:5}, loss: {running_loss / 2000:.6f}"
)
running_loss = 0.0
print(f"Training finished")
Epoch [1/2], batch 2000, loss: 2.108662
Epoch [1/2], batch 4000, loss: 1.737864
Epoch [1/2], batch 6000, loss: 1.592003
Epoch [1/2], batch 8000, loss: 1.507958
Epoch [1/2], batch 10000, loss: 1.445331
Epoch [1/2], batch 12000, loss: 1.393309
Epoch [2/2], batch 2000, loss: 1.327055
Epoch [2/2], batch 4000, loss: 1.302520
Epoch [2/2], batch 6000, loss: 1.286105
Epoch [2/2], batch 8000, loss: 1.265079
Epoch [2/2], batch 10000, loss: 1.240521
Epoch [2/2], batch 12000, loss: 1.270833
Training finished
Model evaluation#
correct = 0
total = 0
with torch.no_grad():
for data in testloader:
# Load inputs and labels
images, labels = data
# Compute model predictions for batch. Shape is (batch size, number of classes) so(4, 10) here
outputs = cnn_model(images)
# Get the indexes of maximum values along the second axis
# This gives us the predicted classes (those with the highest prediction value)
_, predicted = torch.max(outputs.data, dim=1)
total += labels.size(0)
# Add the number of correct predictions for the batch to the total count
correct += (predicted == labels).sum().item()
print(f"Test acccuracy: {(100 * correct / total)}%")
Test acccuracy: 56.16%
Training analysis with TensorBoard#
More info on PyTorch/TensorBoard integration here.




